Cusinu

Datu un triangulu rittangulu, u cusinu d'un angulu acutu hè difinitu com'è u rapportu trà i lunghezzi di u catetu aghjacenti à l'angulu è di l'iputenusa

In matematica, in particulari in trigunumitria, datu un triangulu rittangulu, u cusinu di unu di i dui anguli interni aghjacenti à l'iputenusa hè difinitu com'è u rapportu trà i lunghezzi di u catetu aghjacenti à l'angulu è di l'iputenusa.

Di manera generali, u cusinu d'un angulu $\alpha$, aspressu in gradi o radianti, hè una quantità chì dipendi solu da $\alpha$, custruita usendu a circumfarenza unitaria.

Difiniscendu com'è $\cos (x)$ u valori di u cusinu in l'angulu $x$, s'otteni a funzioni cusinu, una funzioni trigunumetrica di fundamintali impurtanza in l'analisa matematica.

Difinizioni

In u triangulu rossu nantu à a figura, u cusinu di x hè datu da: $\cos x=\overline{OC}$ Più in generali, si difinisci u cusinu pigliendu una circumfarenza di raghju unitariu è una mezaretta chì esci da l'urighjina chì forma un angulu $x$ incù l'assu di l'ascissi com'è nantu à a figura. U cusinu di l'angulu $x$ hè difinitu cusì com'è u valori di a cuurdinata $x$ di u puntu d'intarsizioni trà a mezaretta è a circumfarenza (nantu à a figura, hè a lunghezza di u sigmentu $OC$).

A tavuledda siguenti esponni i principali valori nutevuli assunti da a funzioni cusinu:

$x$ in radianti	0	$\frac{\pi }{6}$	$\frac{\pi }{4}$	$\frac{\pi }{3}$	$\frac{\pi }{2}$	$\pi$	$\frac{3\pi }{2}$	$2\pi$
$x$ in gradi	0°	30°	45°	60°	90°	180°	270°	360°
$\cos (x)$	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$ || 0 || -1 || 0 || 1

Esisti un'antra difinizioni di cusinu in rilazioni à i rutazioni: u cusinu d'un angulu $x$ hè u cumpunenti longu l'assu di l'ascissi di u virsori $i$, virsori di l'assu $x$, ghjiratu di $x$.

Funzioni cusinu

A funzioni cusinu hè difinita assucendu à $x$ u cusinu di l'angulu $x$ (rapprisintatu in radianti), è hè indicata incù $f(x)=\cos x$. Apposta ch'è $x$ è $x+2k\pi$ difiniscini u stessu angulu par qualsiasi $k$ intreiu, a funzioni cusinu hè una funzioni piriodica di periodu $2\pi$ (induva $2\pi$ hè l'angulu ghjiru). A curva di u graficu di sta funzioni hè dinuminata cusinusoidi. L'insemu di variabilità di a funzioni cusinu hè $[-1,1]$, veni à dì applichendu 'ssa funzioni à qualunqua numaru riali s'otteni sempri un numaru riali cumpresu trà $-1$ è $1$, estremi inclusi.

Ripprisintazioni grafica d'una cusinusoidi.

Cusinu è sinu

Valori principali (cusinu, sinu)

Trà sinu è cusinu esisti a rilazioni fundamintali, ditta equazioni fundamintali di a trigunumitria, o unità guniumetrica:

${\sin }^{2}x+{\cos }^{2}x=1,$

chì hè cunsiquenza di u tiurema di Pitagora.

Prubità analitichi di u cusinu

A dirivata di a funzioni cusinu hè l'oppostu di a funzioni sinu. T'avemu dunqua: $(\cos x{)}^{\prime }=-\sin x.$

Quissa pò essa dimustrata applichendu una formula di prustaferesi par calculà a limita di u rapportu incrimintali di u cusinu:

$\frac{\cos (x+h)-\cos x}{h}=\frac{-2\sin \frac{2x+h}{2}\sin \frac{h}{2}}{h}=-\frac{\sin \frac{h}{2}}{\frac{h}{2}}\sin (x+\frac{h}{2})\underset{h\to 0}{⟶}-\sin x$.

A dirivata siconda di u cusinu hè a funzioni stessa cambiata di segnu:

$(\cos x{)}^{\prime \prime }=-\cos x,$

par via di cunsiquenza, a funzioni cusinu com'è a funzioni sinu) risolvi l'equazioni diffarinziali

$y^{\prime \prime }+y=0$,

chì discrivi u motu d'un uscillatori armonicu ideali libaru.

A funzioni cusinu hè una funzioni à dirivati equilimitati (s'hà infatti $|y^{(k)}|\le 1$ per ogni $k$), ed hè par via di cunsiquenza analitica; a so espansioni in seria di Taylor hè: $\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$ $=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{x}^{2n}}{(2n)!}$

par ogni $x$ riali.

In analisa matematica 'ss'ugualità hè à spessu usata par difiniscia u cusinu. Listessa seria difinisci u cusinu com'è funzioni olumorfa annantu à tuttu u pianu cumplessu.

Equazioni fundamintali rilativi à u cusinu

Vali a siguenti formula d'addizioni (è suttrazzioni) d'archi:

$\cos (x\pm y)=\cos x\cos y\mp \sin x\sin y,$

è in particulari a formula di duplicazioni

$\cos (2x)={\cos }^{2}x-{\sin }^{2}x=1-2{\sin }^{2}x=2{\cos }^{2}x-1.$

I siguenti sò i furmuli di prustaferesi rilativi à u cusinu:

$\cos x+\cos y=2\cos \frac{x+y}{2}\cos \frac{x-y}{2},$

$\cos x-\cos y=-2\sin \frac{x+y}{2}\sin \frac{x-y}{2}.$

Vali ancu a catena di disugualità:

$0<x\cos x<\sin x<x\text{ par }0<x<\frac{\pi }{2}.$

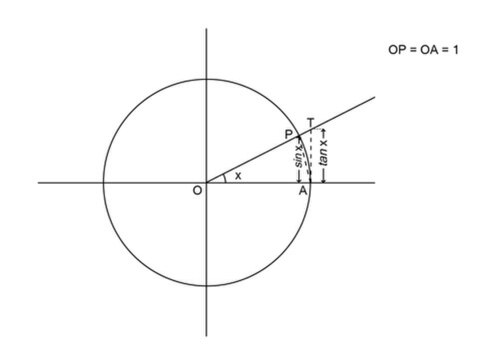
Si cunsidareghja a circumfarenza unitaria, è sii $0<x<\pi /2$, com'è nantu à a figura.

Si tracci a mezaretta chì esci da l'urighjina chì forma un angulu $x$ (antiurariu) rispettu à u mezassu pusitivu di l'ascissi. Tandu i cuurdinati di u puntu d'intarsizioni $P$ di a mezaretta incù a circumfarenza sò $(\cos x,\sin x)$. Si traccia u sigmentu chì unisci $P$ à u puntu $A=(1,0)$. Sii inoltri $T$ u puntu d'intarsizioni trà a mezaretta è a retta d'ascissa $1$ (assu di i tangenti). $T$ hà cuurdinati $(1,\tan x)$.

Si nota ch'è u triangulu $POA$ hè strittamenti rinchjusu in u sittori circulari $POA$, u quali hè rinchjusu strittamenti in u triangulu $TOA$. Vali tandu a disugualità di i rispittivi arii (si ricorda ch'è $x$ hè l'angulu, aspressu in radianti):

$0<\frac{1}{2}\sin x<\frac{1}{2}x<\frac{1}{2}\frac{\sin x}{\cos x},$

veni à dì

$0<\sin x<x<\frac{\sin x}{\cos x}.$

Da a prima parti di a disugualità si ricava ch'è $0<\sin x<x$, mentri cunsidarendu a siconda, dividendu veni à dì par $\sin x$ (ciò chì hè pussibuli parchì $\sin x>0$), s'utteni:

$1<\frac{x}{\sin x}<\frac{1}{\cos x},$

veni à dì

$\sin x\cos x<x\cos x<\sin x,$

induva à a fini s'hè multiplicatu par $\sin x$ è par $\cos x$, ciò chì priserva u versu di a disugualità parchì sò tremindù pusitivi. Ricapitulendu i risultati,

$0<x\cos x<\sin x<x.$

Q.E.D..

}}

Esisti ancu una'idantità trigunumetrica chì metti in rilazioni a funzioni cusinu à a funzioni tangenti:

$\cos x=\frac{1-{\tau }^2}{1+{\tau }^2}\text{ incù }\tau =\tan \frac{x}{2}$.

st'idantità si svela di fundamintali impurtanza in a risuluzioni d'equazioni guniumetrichi in a quali a scunnisciuta figura com'è argumentu sii d'un sinu sii d'un cusinu (o di funzioni dirivati da quiddi). Esisti, infatti, un'idantità analoga par ciò chì riguarda u sinu, ciò chì parmetti a risuluzioni di l'equazioni incù a scunnisciuta $\tau$. Di listessa manera, si pò sfruttà sta rilazioni par u calculu di i primitivi di funzioni guniumetrichi.

Difinizioni currilati

• U reciprocu di u cusinu (difinitu induva u cusinu hè diffarenti da zeru) hè a secanti:

$\sec x=\frac{1}{\cos x}.$

• A funzioni cusinu hè iniettiva nantu à l'intarvallu $[0,\pi ]$ è hà dunqua una inversa, chjamata arcucusinu (indicatu incù $\arccos$ o incù ${\cos }^{-1}$ chì ripiglia a nutazioni di a funzioni inversa).

Urighjina di u nomu

U terminu cusinu stà par "cumplimintariu di u sinu". Infatti, par anguli trà $0$ è $\pi /2$, u cusinu d'un angulu hè u sinu di l'angulu cumplimintariu, veni à dì :$\cos x=\sin (\frac{\pi }{2}\pm x).$ sta rilazioni, chì si ricava da i furmuli di somma d'archi, hè valida par ogni $x$; eppuri a nuzioni giumetrica d'angulu cumplimintariu s'applicheghja solu l'anguli pusitivi, è dunqua cumpresi trà $0$ è $\pi /2$.

Da veda dinò

• Sinu
• Leghji di u cusinu
• Cusinusoidi
• Funzioni trigunumetrica
• Tangenti (matematica)
• Arcucusinu
• Circumfarenza guniumetrica
• Formula di Eulero
• Formuli di duplicazioni
• Formuli di bisizzioni
• Formuli di prustaferesi
• Formuli di Werner
• Funzioni piriodica
• Funzioni altirnata
• Cusinu iperbolicu

Fonti

'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.